
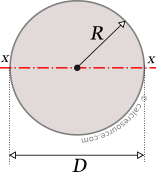
A new axis of rotation ends up with a different formula, even if the physical shape of the object remains the same. The moments of inertia had to reference the same axis. In this derivation, we have to follow certain steps. The moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle. The consequence of this formula is that the same object gets a different moment of inertia value, depending on how it is rotating. Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression I R 4 / 4 Here, R is the radius and the axis is passing through the centre. For the derivation of the moment of inertia formula of a circle, we will consider the circular cross-section with the radius and an axis passing through the centre.
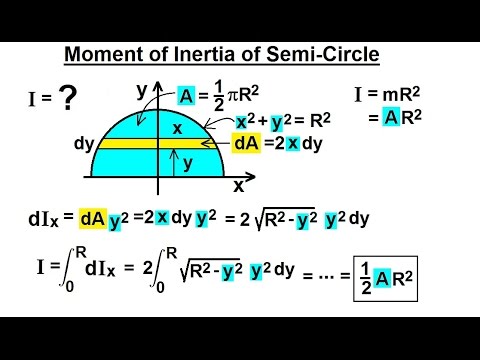
That point mass relationship becomes the basis for all other moments of inertia since any object can be built up from a collection of point masses. In this case, the summation over the masses is simply because the two masses at the end of the barbell can be approximated as point masses, and the sum, therefore, has only two terms. For a p oint mass the moment of inertia is just the mass times the square of perpendicular distance to the rotation axis, I mr2, where m is mass and r radial (joining by a straight line) distance from axis about which moment of inertia is being calculated. To see this, let’s take a simple example of two masses at the end of a massless (negligibly small mass) rod and calculate the moment of inertia about two different axes. How we can find the centre of mass of Earth by using concept of moment of inertia? By the end of this section, you will be able to: Calculate the moment of inertia for uniformly shaped, rigid bodies Apply the parallel axis theorem to find the. The moment of inertia of a uniform semicircular ring of mass M and radius R about the axis perpendicular to plane of ring is 1 ? Using Above Formula You can solve Following types of Question -: Because rr is the distance to the axis of rotation from each piece of mass that makes up the object, the moment of inertia for any object depends on the chosen axis. We defined the moment of inertia I of an object to be for all the point masses that make up the object. Moment of inertia of the particle about - axis If we divide the whole lamina into a number of particles of masses at distances from the axis.


 0 kommentar(er)
0 kommentar(er)
